Финальное задание
Написать функцию relax(G), используя библиотеку Cirq, и показать использование
функции (при помощи тестов или обычных вызовов).
Постановка задачи
На вход функции подаётся описание ориентированного взвешенного графа \(G\) без петель в виде матрицы смежности. Гарантируется, что данные корректны. Веса рёбер являются положительными целыми числами, число 0 в матрице обозначает отсутствие ребра.
Функция должна найти с достаточно высокой вероятностью любую такую пару вершин \(s\) и \(t\), что между ними нет ребра, но существует такая вершина \(u\), что есть рёбра \(s \to u\) и \(u \to v\). Если таких вершин нет, функция должна об этом просигнализировать.
Функция должна существенным образом использовать квантовые вычисления.
Пример
Например,
import cirq # import what-you-need-to-import def relax(G): # your code here pass s,t = relax([ [ 0, 5, 0, 4 ], [ 3, 0, 1, 0 ], [ 2, 0, 0, 6 ], [ 0, 0, 7, 0 ] ]) print(s,t)
Входные данные
Здесь в s,t должна быть пара вершин.
В примере граф выглядит так:
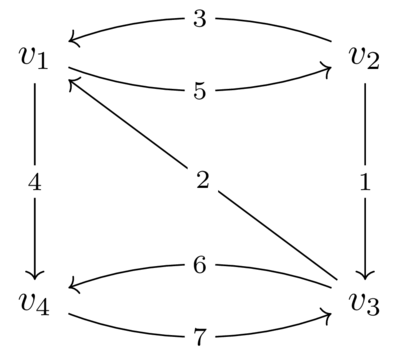
Возможные ответы
В графе между следующими вершинами нет рёбер:
- от \(v_1\) к \(v_3\),
- от \(v_2\) к \(v_4\),
- от \(v_3\) к \(v_2\),
- от \(v_4\) к \(v_1\),
- от \(v_4\) к \(v_2\).
Поэтому в качестве ответа можно выдать любую пару из:
- 1,3 — есть путь \(v_1 \to v_2 \to v_3\),
- 2,4 — есть пути \(v_2 \to v_3 \to v_4\) и \(v_2 \to v_1 \to v_4\),
- 3,2 — есть путь \(v_3 \to v_1 \to v_2\),
- 4,1 — путь \(v_4 \to v_3 \to v_1\).
Нет путей из двух рёбер между 4 и 2, поэтому этот ответ не должен выдаваться.