Алгоритм Саймона
Задача нахождения периода
Пусть задана функция \(f: \{0,1\}^n \to \{0,1\}^n\) (в виде оракула), т.е. функция, которая каждой последовательности из \(n\) бит ставит в соответствие последовательность из \(n\) бит.
Гарантируется, что выполняется следующее условие. Функция устроена так, что для какого-то (неизвестного нам) \(s \in \{0,1\}^n\) и для всех \(x,y \in \{0,1\}^n\) выполняется, что \[ f(x) = f(y) \iff x \oplus y \in \{0^n, s\}, \] где \(\oplus\) — побитовое исключающее «или» (XOR).
В задаче требуется найти период \(s\), используя как можно меньше запросов к функции \(f\).
Заметим, что если \(s \neq 0^n\), то функция выдаёт один и тот же результат для двух разных значений только если они отличаются на \(s\): \(f(x) = f(x \oplus s)\), т.е. функция периодична с периодом \(s\).
Ещё одно наблюдение — если \(s = 0^n\), то функция задаёт перестановку (т.е. отображает различные входные значения в различные выходные), и для каждого выходного значения есть ровно одно входное значение, которое ему соответствует (функция является отображением «1-к-1», one-to-one). Если же \(s \neq 0^n\), то у каждого выходного значения есть ровно два входных значения, которые ему соответствуют (функция является отображением «2-к-1», two-to-one).
Классический алгоритм
Для решения задачи на классическом компьютере требуется не меньше \(\Omega(\sqrt{2^n})\) вычислений \(f\) (находим коллизию, используя парадокс дней рождений)
Квантовый алгоритм Саймона
В квантовом случае используется следующая схема
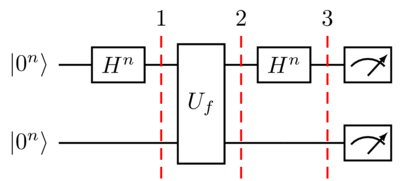
Что будет получено в результате запуска?
Состоянием после применения оператора Адамара будет:
\begin{equation*} |\Psi_1\rangle = \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1} \big( |x\rangle \otimes |0^n\rangle \big) \end{equation*}Оракул \(U_f\) для функции \(f\) добавляет ко второму регистру результат вычисления \(f(x)\) и делает это одновременно для всех возможных значений \(x\):
\begin{equation*} |\Psi_2\rangle = \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1} \big( |x\rangle \otimes |f(x)\rangle \big) \end{equation*}После применения второго оператора Адамара, получим следующее состояние:
\begin{equation*} |\Psi_3\rangle = \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1} \Big( \frac{1}{\sqrt{2^n}}\sum_{y=0}^{2^n-1} (-1)^{x\cdot y} |y\rangle \Big) \otimes |f(x)\rangle, \end{equation*}где \(x \cdot y = x_1 y_1 \oplus x_2 y_2 \oplus \ldots x_n y_n \) — скалярное произведение \(x\) и \(y\) по модулю 2.
Это состояние можно переписать следующим образом (поменяв местами суммы по \(x\) и \(y\)):
\begin{equation*} |\Psi_3\rangle = \frac{1}{2^n}\sum_{y=0}^{2^n-1} \Big( |y\rangle \otimes \sum_{x=0}^{2^n-1} (-1)^{x\cdot y} \otimes |f(x)\rangle \Big) \end{equation*}Далее нам необходимо выполнить измерение регистров. Рассмотрим два возможных случая из условия задачи: \(x \oplus y = 0^n\) и \(x \oplus y = s, s \neq 0^n\).
Случай \(s = 0^n\)
В этом случае функция задаёт перестановку.
Вероятность получить какую-либо строку \(y \in \{0,1\}^n\) в первом регистре равна:
\begin{equation*} p_y = \frac{1}{2^n} \| \sum_{x=0}^{2^n-1} (-1)^{x\cdot y} |f(x)\rangle \|^2 = \frac{1}{2^n} \| \sum_{x=0}^{2^n-1} (-1)^{x\cdot y} |x\rangle \|^2 = \frac{1}{2^n}, \end{equation*}где второе равенство получается, поскольку \(f(x)\) пробегает все те же значения, что и \(x\), только, возможно, в другом порядке.
В итоге при измерении будет получена произвольная строка \(y \in \{0,1\}^n\) с одной и той же вероятностью \(2^{-n}\) для любой \(y\).
Случай \(s \neq 0^n\)
В этом случае функция задаёт отображение «2-к-1».
Пусть \(A = f(\{0,1\}^n)\) — образ \(f\), множество всех возможных результатов, которые могут быть получены при вычислении \(f\). Тогда для каждого значения \(x_1 \in \{0,1\}^n\) существует ровно одно \(x_2 \in \{0,1\}^n\) такое, что \(f(x_1) = f(x_2) = z \in A\); более того, \(x_2 = x_1 \oplus s\).
Тогда получаем, что вероятность получить \(y \in \{0,1\}^n\) при измерении равна:
\begin{equation*} p_y = \frac{1}{2^n} \| \sum_{x=0}^{2^n-1} (-1)^{x\cdot y} |f(x)\rangle \|^2 = \frac{1}{2^n} \| \sum_{z \in A} \big( (-1)^{x_1 \cdot y} + (-1)^{x_2 \cdot y} \big) |z\rangle \|^2. \end{equation*}Поскольку \(x_2 = x_1 \oplus s\), получаем, что коэффициент при состоянии \(z\) равен \[ (-1)^{x_1 \cdot y} + (-1)^{x_2 \cdot y} = (-1)^{x_1 \cdot y} + (-1)^{(x_1 \oplus s) \cdot y} = (-1)^{x_1 \cdot y} (1 + (-1)^{s \cdot y}). \]
Если \(s \cdot y = 1\), то \(p_y = 0\). Подобное поведение называется деструктивной интерференцией: мы запускали одновременное вычисление в нескольких ветках (в нескольких Вселенных, если верить многомировой интерпретации), а потом некоторые из них «схлопнулись», не оставив и следа.
Если \(s \cdot y = 0\), то \(p_y = \frac{1}{2^{n-1}}\). Это называется конструктивной интерференцией.
Получаем, что мы можем измерить только такие \(y\), что \(y \cdot s = 0\).
Классический пост-процессинг результатов
Запустим схему \(n\) раз подряд и получим разные строки \(y_1, \ldots, y_n\).
Далее мы можем составить систему из уравнений вида \(y_j \cdot s = 0\), где \(s\) будет вектором неизвестных. Решая её, мы придём к одному из вариантов: либо система неразрешима — тогда \(s = 0^n\), либо мы найдём её решение \(s \neq 0^n\) (и оно с вероятностью \(>1/4\) будет единственным).
Значение
Квантовый алгоритм работает экспоненциально быстрее: \(O(n)\) вычислений функции вместо \(\Omega(\sqrt{2^n})\). Кроме того, задача, в отличие от задачи Дойча-Йожи, выглядит более «практической»: её можно применить, например, в криптографии. Развитие этих идей привело к появлению алгоритма Шора — алгоритма для разложения числа на простые сомножители (т.е. взлома RSA и сходных алгоритмов).
Кроме того, алгоритм можно модифицировать, чтобы он работал и для тех функций, где период «примерный», т.е. условие \(f(x) = f(x \oplus s)\) выполняется не во всех, а в большой доле случаев.