Алгоритмы Дойча и Дойча-Йожи
Задача
На вход алгоритму подаётся функция \(f: \{0,1\}^n \to \{0,1\}\) (заданная в виде оракула \(U_f\)).
Гарантируется, что функция \(f\) принадлежит одному из двух классов:
- либо она константная, т.е. на всех входных данных возвращает 0 или на всех входных данных возвращает 1;
- либо она сбалансированная, т.е. ровно на половине входных данных она возвращает 0, а на другой половине — 1.
Алгоритм должен ответить, какому классу принадлежит функция.
Значение
Как легко заметить, классический алгоритм в худшем случае должен выполнить \(2^{n-1} + 1\) запрос к оракулу, так как ему нужно проверить более половины входных данных.
Оказывается, что квантовый алгоритм может решить эту задачу всего за одно (!) обращение к оракулу.
Алгоритм Дойча
Первоначально Дэвид Дойч (David Deutch) сформулировал эту задачу и её решение — алгоритм Дойча — для \(n=1\). Мы рассмотрим обобщение задачи и решения на случай произвольного \(n\).
Алгоритм Дойча-Йожи
Алгоритм Дойча-Йожи (Deutch-Jozsa) работает следующим образом.
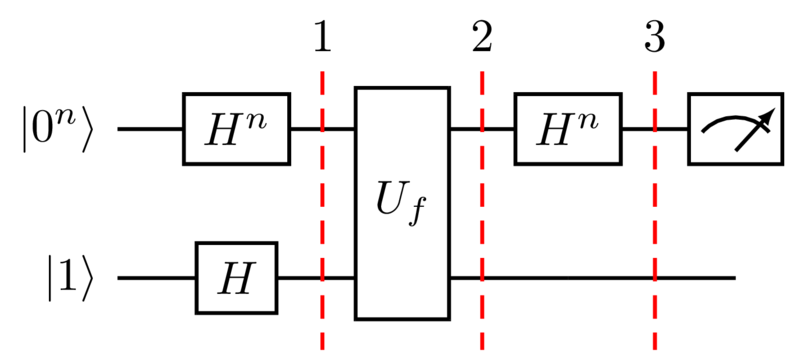
Проверим, какие состояния получаются на каждом шаге алгоритма (соответствующие позиции отмечены красными штриховыми линиями на схеме).
Начальное состояние, подаваемое на вход алгоритму таково:
\begin{equation*} |\Psi_0\rangle = |0^n\rangle |1\rangle \end{equation*}После применения операторов Адамара получаем:
\begin{equation*} |\Psi_1\rangle = \frac{1}{\sqrt{2^{n+1}}}\sum_{x=0}^{2^n-1}|x\rangle (|0\rangle - |1\rangle) \end{equation*}После применения оракула \(U_f\) получаем такое состояние (если не очевидно — вспомните преобразование из раздела об оракулах):
\begin{equation*} |\Psi_2\rangle = \frac{1}{\sqrt{2^{n+1}}}\sum_{x=0}^{2^n-1}(-1)^{f(x)}|x\rangle (|0\rangle - |1\rangle) \end{equation*}Поскольку последний кубит не зависит от индекса, по которому идёт суммирование, мы можем его игнорировать, состояние распадается на произведение
\begin{equation*} |\Psi_2\rangle = |\Psi'_2\rangle \otimes \frac{1}{\sqrt{2}} (|0\rangle - |1\rangle), \end{equation*}где
\begin{equation*} |\Psi'_2\rangle = \frac{1}{\sqrt{2^n}} \sum_{x=0}^{2^n-1} (-1)^{f(x)} |x\rangle. \end{equation*}Чтобы понять, какое состояние получится, рассмотрим отдельное базисное состояние и подсчитаем, что получится в результате применения оператора Адамара к нему:
\begin{equation*} H^n |x\rangle = \frac{1}{\sqrt{2^n}} \sum_{y=0}^{2^n-1} (-1)^{s(x,y)} |y\rangle, \end{equation*}где \(s(x,y)\) — либо 0, либо 1.
Давайте поймём, что такое \(s(x,y)\). Если в \(x\) все биты нулевые, то \(s(0^n, y) = 0\), т.е. знак положительный при всех слагаемых \(y\). Если в \(x\) ровно один бит единичный, то он даст множитель со знаком «минус» — если в \(y\) на этом месте стоит единица. Если таких битов несколько — «минусы» будут перемножаться.
Надеюсь, мне удалось убедить вас в том, что \(s(x,y) = x\cdot y = x_1 y_1 \oplus x_2 y_2 \oplus \ldots \oplus x_n y_n\). Строгое доказательство этого остаётся вам в качестве упражнения.
Таким образом, после применения операторов Адамара к состоянию 2 и перегруппировки слагаемых, получаем:
\begin{equation*} |\Psi_3\rangle = \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}(-1)^{f(x)} \Big( \frac{1}{\sqrt{2^n}} \sum_{y=0}^{2^n-1} (-1)^{x\cdot y} |y\rangle \Big) = \end{equation*} \begin{equation*} = \frac{1}{2^n} \sum_{x=0}^{2^n-1} \sum_{y=0}^{2^n-1} (-1)^{f(x) + x\cdot y} |y\rangle = \end{equation*} \begin{equation*} = \frac{1}{2^n} \sum_{y=0}^{2^n-1} \Big(\sum_{x=0}^{2^n-1} (-1)^{f(x) + x\cdot y} \Big) |y\rangle. \end{equation*}Что может быть получено в результате измерения? Вычислим вероятность того, что будут получены все нули (\(y=0^n\)):
\begin{equation*} p = \Pr[\mathcal{M}|\Psi_3\rangle = 0^n] = \Big| \frac{1}{2^n} \sum_{x=0}^{2^n-1} (-1)^{f(x)} \Big|^2. \end{equation*}Здесь возможны два случая: \(f\) — константная или \(f\) — сбалансированная.
Пусть \(f\) — константная. Тогда все \((-1)^{f(x)}\) равны (либо \(1\), либо \(-1\)), поэтому сумма в целом равна \(2^n\) и вероятность \(p\) равна 1.
Пусть \(f\) — сбалансированная. Тогда ровно половина слагаемых равна \(1\), а вторая половина равна \(-1\). Эти слагаемые взаимно сокращаются, и вероятность \(p\) получается равной 0.
В итоге мы наблюдаем следующее поведение. Если \(f\) — константная, то в результате выполнения этой схемы мы всегда будем получать \(0^n\); если \(f\) — сбалансированная, то мы никогда не получим \(0^n\), а получим какой-то другой результат.
Как видно на схеме, оракул применяется в ней один раз, поэтому на квантовом компьютере мы решаем задачу за одно вычисление функции \(f\) вместо \(\Omega(2^n)\) вычислений в классическом случае.