Квантовое преобразование Фурье
Преобразование Фурье
Вероятно, вам знакомо преобразование Фурье, которое, неформально говоря, преобразует функции от времени \(f(x)\) в функции от частоты \(\hat{f}(\xi)\), т.е. раскладывает функцию в частотный спектр: \[ \hat{f}(\xi) = \int_{-\infty}^\infty f(x) e^{-i 2\pi\xi x}\,dx. \] Результат преобразование, грубо говоря, показывает, какая амплитуда \(\hat{f}(\xi)\) должна быть у синусоиды с соответствующей частотой \(\xi\), чтобы в результате сложения получилась оригинальная функция \(f(x)\).
Если функция \(f\) задана в виде таблицы значений \(\{x_n\} = \{x_0, \ldots, x_{N-1}\}\), а не формулой, вы тоже можете вычислить (с соответствующей точностью) таблицу значений \(\{y_k\} = \{y_0, \ldots, y_{N-1}\}\) образа \(\hat{f}\), для этого используется дискретное преобразование Фурье (DFT, Discrete Fourier Transform): \[ y_k = \sum_{n=0}^{N-1} x_n e^{-\frac{i2\pi}{N}kn} = \sum_{n=0}^{N-1} x_n \bigg( \cos \Big( \frac{2\pi}{N}kn \Big) - i \sin \Big( \frac{2\pi}{N}kn \Big) \bigg). \] Для более эффективного вычисления этой таблицы используется алгоритм быстрого преобразования Фурье (FFT, Fast Fourier Transform).
Для удобства обозначим корень \(N\)-й степени из единицы как \(\omega_N = e^{2i\pi / N}\).
Квантовое преобразование Фурье
Квантовое преобразование Фурье является способом вычислить дискретное преобразование Фурье на квантовом компьютере. Для этого коэффициенты \(\{x_k\}\) и \(\{y_k\}\) записываются как амплитуды соответствующих состояний \(|k\rangle\). Пусть \(|X\rangle = \sum_{j=0}^{N-1} x_j |j\rangle\) и \(|Y\rangle = \sum_{k=0}^{N-1} y_k |k\rangle\). Тогда достаточно придумать способ эффективного вычисления преобразования \[ \vert j \rangle \mapsto \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} \omega_N^{jk} |k\rangle, \] чтобы получить необходимое.
На квантовое преобразование Фурье можно взглянуть и с иной точки зрения. Можно считать, что это замена базиса для счёта. Если в обычном базисе счёт выполняется изменением значений битов («0001» сменяется на «0010», на «0011», и т.д.), причём младший бит меняется каждый раз, следующий — раз в два такта, следующй — раз в четыре и т.д., то в базисе Фурье вместо этих изменений происходят вращения вокруг оси Z. Младший кубит на каждом такте поворачивается на полоборота (делает полный оборот за два такта), следующий делает оборот за четыре, следующий — за восемь и т.д.:
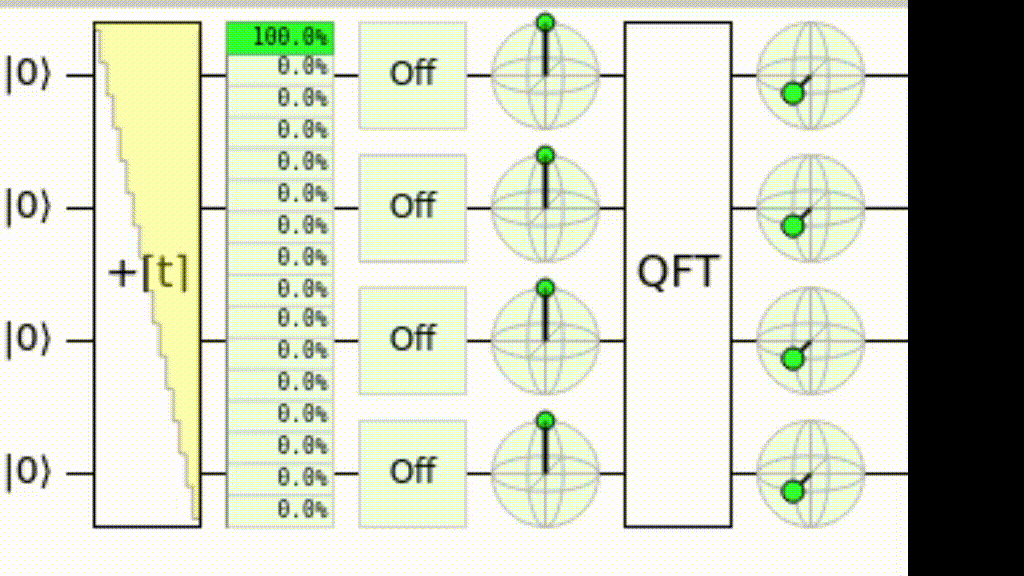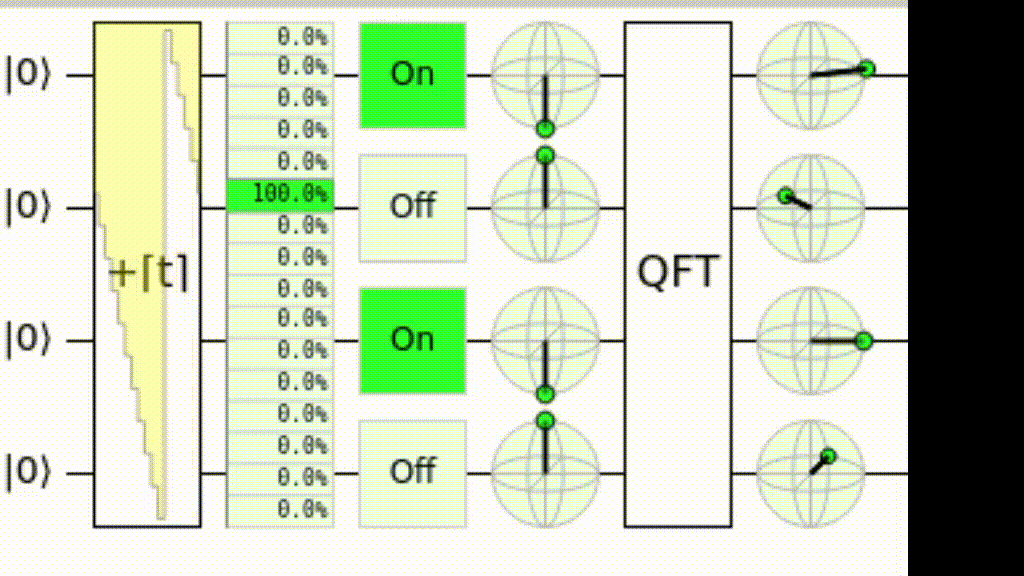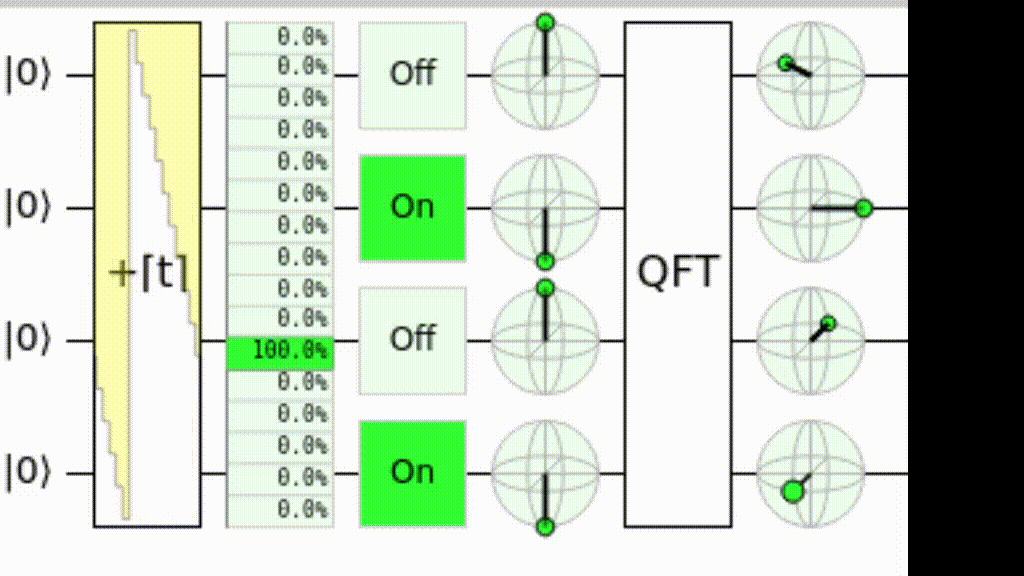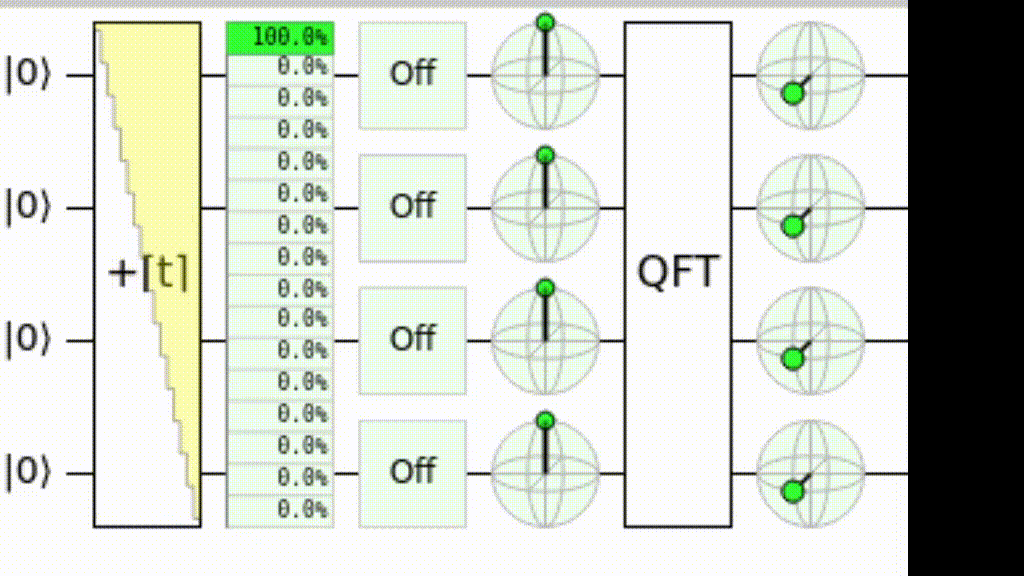
Схема для QFT
Это же наблюдение подсказывает и то, как можно вычислить квантовое преобразование Фурье в виде схемы. Пусть \(N = 2^n\):
\begin{align*} QFT_N|x\rangle &= \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1} \omega_N^{xy} |y\rangle = \\ &= \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1} e^{2\pi i xy / 2^n} |y\rangle. \end{align*}Записывая \(y\) в виде последовательности отдельных битов \(y_k\) и учитывая, что \(y / 2^n = \sum_{k=1}^n y_k / 2^k\), получаем:
\begin{align*} QFT_N|x\rangle &= \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1} e^{2\pi i x \sum_{k=1}^n y_k / 2^k} |y_1 y_2 \ldots y_n\rangle = \\ &= \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1} \prod_{k=1}^n e^{2\pi i x y_k / 2^k} |y_1 y_2 \ldots y_n\rangle = \\ &= \frac{1}{\sqrt{N}} \bigotimes_{k=1}^{n} \big(|0\rangle + e^{2\pi i x / 2^k} |1\rangle \big). \end{align*}Соответствующая схема будет выглядеть так:
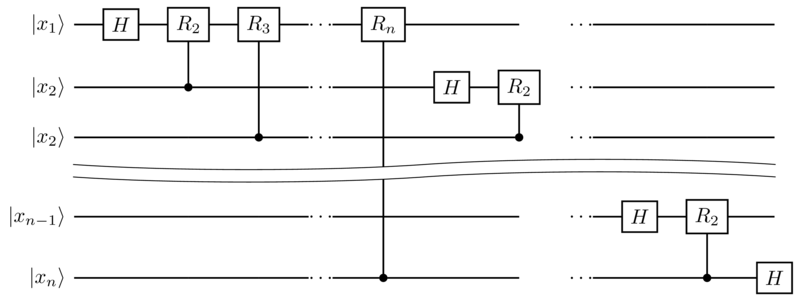
Выглядит довольно сложно для того, чтобы собирать мышкой. Давайте напишем код для этого!
Код для QFT
Нам потребуется гейт для оператора \(CR_j\), который является степенью оператора \(CZ\): \(CR_j = CZ^{1/2^{j-1}}\). К счастью, в Cirq уже есть возможность возводить операторы в степень, и это делается естественным образом: cirq.CZ ** (1/2**k).
В итоге код выглядит следующим образом:
import cirq def make_qft(qubits): qreg = list(qubits) while len(qreg) > 0: q_head = qreg.pop(0) yield cirq.H(q_head) for i, qubit in enumerate(qreg): yield (cirq.CZ ** (1/2**(i+1)))(qubit, q_head)
Попробуем вывести схему и проверим, правильно ли она выглядит:
qubits = cirq.LineQubit.range(4) qft = cirq.Circuit(make_qft(qubits)) print(qft)
Разумеется, каждый раз писать вручную этот код не нужно. Эта функция уже реализована в cirq под названием cirq.qft.