Оракулы
Чтобы соединить классический мир битов с квантовым нужно каким-то образом закодировать классические данные. При этом кодирование должно быть таким, чтобы эти данные можно было использовать в квантовых схемах (например, запускать одни и те же вычисления для разных классических данных). Это исключает возможность, например, контроля с использованием классических битов — внести данные один раз так, конечно, можно, но для перебора разных вариантов потребуется многократно вносить классические данные.
Для кодирования используют т.н. «оракулы» — квантовые гейты, преобразование которых зависит от классических данных, например, от входных данных задачи. Можно считать, что достаточно иметь возможность закодировать произвольную функцию \(f: \{0,1\}^n \to \{0,1\}\), т.е. функцию, которая отмечает какие-то битовые наборы из \(n\) битов. Если на выходе требуется больше битов — то можно просто сделать несколько подобных оракулов.
Два способа моделирования и перевод одного в другой
Оракулы, как правило, используют один из двух способов кодирования функции \(f\).
При первом способе оракул меняет знак тех базовых состояний, которые «помечены» функцией \(f\):
\begin{equation*} |x\rangle \mapsto (-1)^{f(x)} |x\rangle, \end{equation*}При втором способе оракул использует вспомогательный кубит (ancilla), к значению которого добавляет значение функции на входном состоянии:
\begin{equation*} |x\rangle |y\rangle \mapsto |x\rangle |y \oplus f(x)\rangle. \end{equation*}Эти способы эквивалентны друг другу: один можно преобразовать в другой. Пусть, к примеру, оракул \(O_2\) задаёт функцию вторым способом. Тогда можно построить оракул \(O_1\), задающий ту же функцию первым способом, применив \(O_2\) к состоянию
\begin{equation*} |x\rangle \otimes \frac{1}{\sqrt 2} \big( |0\rangle - |1\rangle \big) \end{equation*}Теорема о запрете клонирования
Почему во втором способе используется вспомогательный кубит? Почему нельзя «присвоить» значение \(f(x)\) во вспомогательный кубит?
Всё дело в унитарности. Если бы мы могли уничтожить старое значение, мы могли бы и скопировать значение, т.е. могли бы реализовать следующее преобразование \(U_{copy}\):
\begin{equation*} U_{copy} |x\rangle |y\rangle = |x\rangle |x\rangle. \end{equation*}Используя это преобразование можно было бы копировать произвольные состояния и получать всю информацию, которая в них хранится. Но подобное преобразование невозможно, поскольку верна теорема о запрете клонирования:
Не существует унитарного оператора \(U\), такого, что для любых состояний φ и e
\begin{equation*} U \big( |\phi\rangle \otimes |e\rangle \big) = e^{i\alpha(\phi,e)}|\phi\rangle \otimes |\phi\rangle, \end{equation*}где \(\alpha(\phi,e)\) — вещественное число, зависящее только от \(\phi\) и \(e\).
Допустим, что подобный унитарный оператор \(U\) существует.
Рассмотрим произвольные состояния φ и ψ и следующее скалярное произведение:
\begin{equation*} \langle \phi | \psi \rangle \langle e | e \rangle = \langle \phi | \langle e | e \rangle | \psi \rangle = \langle \phi | \langle e | U^\dagger U | e \rangle | \psi \rangle = \end{equation*} \begin{equation*} = e^{i\alpha(\psi,e) - i\alpha(\phi,e)} \langle \phi | \langle \phi | \psi \rangle | \psi \rangle = e^{i\alpha(\psi,e) - i\alpha(\phi,e)} \big( \langle \phi | \psi \rangle \big)^2. \end{equation*}Получаем, что
\begin{equation*} \big| \langle \phi | \psi \rangle \big| = \big| \langle \phi | \psi \rangle \big|^2. \end{equation*}Но тогда это скалярное произведение равно либо \(0\), либо \(1\). Получаем противоречие с тем, что мы выбрали состояния \(\psi\) и \(\phi\) произвольным образом.
Пример кодирования оракула
Для задания оракулов удобно использовать \(C^nX\)-гейты (например, CNOT, CCNOT и т.п.).
Давайте зададим оракул, которому на вход могут подаваться числа от 0 до 15, и который помечает элемент 11. Мы считаем, что старшие биты находятся сверху, а младшие снизу. Таким образом, нам нужна схема, которая получает на вход пять кубитов (четыре входных и самый нижний — вспомогательный для ответа), и помечает элемент \(1011\) (в двоичной системе \(11_{10} = 1011_{2}\)).
Оракул \(U_{11}\) должен работать следующим образом. Все состояния, кроме следующих двух, не меняются:
\begin{equation*} U_{11} |10110\rangle = |10111\rangle, \end{equation*} \begin{equation*} U_{11} |10111\rangle = |10110\rangle. \end{equation*}Видим, что оракул должен инвертировать последний бит, если первые четыре установлены в 1011, соответственно. Получаем следующую схему (в quirk). Убедитесь, что этот оракул работает правильно.
Для других оракулов, разумеется, могут потребоваться другие контроли или несколько \(C^nX\)-гейтов.
Универсальный классический гейт
Для некоторых оракулов может потребоваться реализовать классическую функцию. Например, оракул может проверить, есть ли между двумя вершинами графа путь, проходящий через третью — для этого нужно вычислить функцию «И» от значений в (заданной) таблице смежности графа. Или оракул может проверить, является ли число суммой двух других — для этого нужно уметь вычислять арифметические операции (от чисел с заданным количеством бит).
Как вам, вероятно, известно из курса дискретной математики, любую булеву функцию можно задать, используя схемы из конечного числа видов элементов (например, «И», «ИЛИ», «НЕ»). Оказывается, чтобы квантовая схема могла вычислить классическую булеву функцию \(L\), достаточно, чтобы эта функция была обратимой.
Функция \(L: \{0,1\}^n \to \{0,1\}^m\) называется обратимой, если существует функция \(L': \{0,1\}^m \to \{0,1\}^n\) такая, что для произвольного \(x\) выполняется условие \(L(x) = y\), то \(L'(y)=x\).
Функция \(L'\) называется обратной для функции \(L\).
Произвольную булеву функцию \(f\) можно преобразовать в обратимую функцию \(F\), если использовать вспомогательный вход: \(F(x,y) = (x,y \oplus f(x))\). Этот приём мы уже видели при задании оракула.
Произвольную обратимую функцию можно построить из нескольких гейтов Тоффоли (гейтов CCNOT) и вспомогательных входных битов, установленных в 0 или 1 — гейт Тоффоли является универсальным гейтом.
Также универсальным гейтом является гейт Фредкина — гейт Controlled-SWAP.
Восстановление вспомогательных кубитов
После использования вспомогательных кубитов нужно вернуть их в исходное состояние.
Для этого используется приём, называемый «uncomputation» — «обратное вычисление». После конечного преобразования с целевым кубитом (куда записывается итоговый результат) над вспомогательными кубитами выполняются обратные к промежуточным преобразования (в обратном порядке).
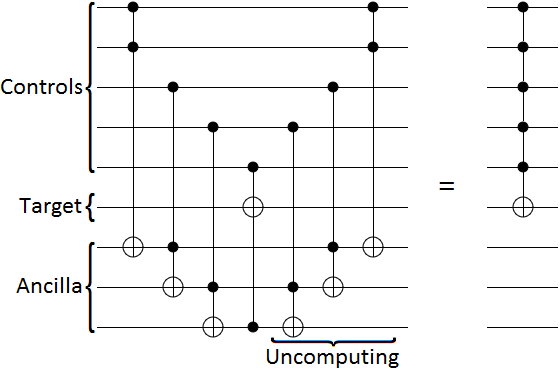
Таким образом, промежуточные преобразования, повлиявшие на значения вспомогательных кубитов, будут «развычислены», т.е. будет дополнительно выполнено обратное преобразование, и вспомогательные кубиты вернутся в исходное состояние.
После обратного вычисления вспомогательные кубиты никак не связаны с основным квантовым регистром, и могут быть переиспользованы в других вычислениях.