Quantum Approximate Optimization Algorithm

Вариационные алгоритмы могут применяться и для решения задач оптимизации. Для этого задачу оптимизации представляют в виде гамильтониана и находят его минимальное собственное число. Одним из алгоритмов для этого является QAOA. Он заключается в том, чтобы разделить гамильтониан на две части: для целевой функции \(H_C\) и для смешивания \(H_M\). Далее для них (классическим образом) подбираются параметры, которые минимизируют результат измерения. Оптимальные значения параметров дают ответ на исходную задачу.

Пример задачи

Рассмотрим задачу Vertex Cover (минимальное вершинное покрытие). Нам дан граф \(G = (V,E)\); требуется выбрать минимальное подмножество вершин \(X \subseteq V\) такое, что каждое ребро инцидентно хотя бы одной выбранной вершине: \[ \forall (a,b) \in E \quad \big( a \in X \vee b \in X \big). \] Минимальное оно, конечно, в смысле количества вершин в подмножестве \(X\). Для некоторых графов возможно несколько минимальных вершинных покрытий. Эта задача является NP-полной.

Будем представлять выбранные вершины в виде двоичных строк (а их — значениями кубитов). Например, если в графе на рисунке пронумеровать вершины сверху вниз и слева направо, то отмеченные вершины будут представляться строкой 01100. 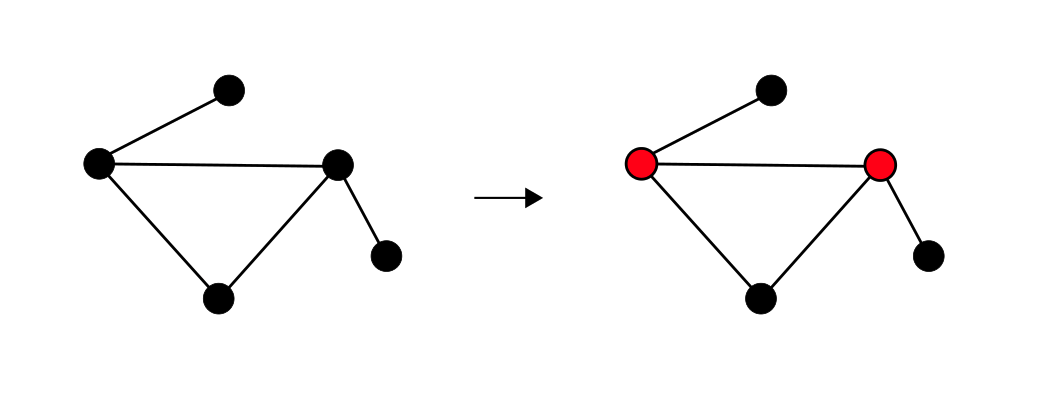qaoa-minvc.png Отмеченное подмножество — минимальное вершинное покрытие для этого графа.

Гамильтонианы

В качестве гамильтониана для смешивания \(H_M\) часто выбирают сумму операторов Паули \(X_j\) по всем кубитам: \[ H_M = \sum_j X_j \]

Целевая функция должна становиться больше, если оба конца ребра не отмечены. Таким образом, для каждого ребра \((u,v)\) нам нужно добавить член вида \(3 (Z_u Z_v + Z_u + Z_v)\). Чтобы искать наименьшее покрытие, добавим ещё член вида \(-Z_v\) для каждой вершины \(v\): \[ H_C = 3 \sum_{(u,v) \in E} (Z_u Z_v + Z_u + Z_v) - \sum_{v \in V} Z_v \]

Оптимизация

Далее, выполняется оптимизация параметров и моделирование унитарной эволюции под действием описанных гамильтонианов. Для этого создаётся схема из нескольких слоёв:

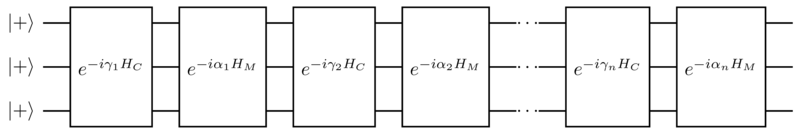
circ-qaoa.png

Параметры \(\gamma = (\gamma_1, \gamma_2, \dots, \gamma_n)\) и \(\alpha = (\alpha_1, \alpha_2, \dots, \alpha_n)\) подбираются классическим образом.

Результирующее состояние должно кодировать минимальное вершинное покрытие.