Qauntum Machine Learning
После применения для задач оптимизации естественно попытаться применить вариационные алгоритмы в машинном обучении. Как правило, различие между квантовыми алгоритмами в задачах оптимизации и машинном обучении лежит в отношении к данным: для квантового машинного обучения характерен больший упор на тренировку на входных данных. Например, параметризованные квантовые схемы называют квантовыми нейронными сетями, если их применяют для анализа данных.
Разумеется, как и вся область, квантовое машинное обучение переживает бурный рост и существует множество алгоритмов, подходов и теоретических исследований. Мы сосредоточимся на одном подходе, который называется Quantum Kernel Methods, квантовые ядерные методы. Как и в других подходах, идея заключается в вычислении ядерной функции на квантовом компьютере в надежде, что отображение входных данных относительно низкой размерности в промежуточное гильбертово пространство экспоненциально большой размерности поможет разделить и классифицировать данные.
Quantum Kernel Method
Пусть задан набор примеров \(\{(\vec{x}_i, y_i)\}\). Алгоритм будет оптимизировать веса \(w_i\) примеров. Для предсказания на новом примере \(\vec{x}'\) он использует функцию сходства (ядро) \(k(\vec{x}_i, \vec{x}')\) между новым примером и тренировочными.
Например, для бинарной классификации можно использовать взвешенную сумму сходств: \[ \hat{y} = \mathrm{sgn} \sum_{i=1}^n w_iy_ik(\vec{x}_i, \vec{x}'), \] где \(\hat{y}\in\{-1,+1\}\) — предсказание для \(\vec{x}'\).
Поскольку метод разработан для классических функций, а в квантовом методе заменяется только ядро, алгоритмы легко приспособить, заменив вычисление функции сходства на квантовое вычисление.
В качестве ядра для квантового метода обычно выбирают перекрытие двух состояний, т.е. каждый пример \(\vec{x}_i\) будет кодироваться состоянием \(\ket{\psi(\vec{x}_i)}\), и для вычисления сходства нужно будет вычислить \(k(\vec{x},\vec{x}') = \langle \psi(\vec{x}) | \psi(\vec{x}') \rangle\).
Это легко сделать при помощи простой схемы:
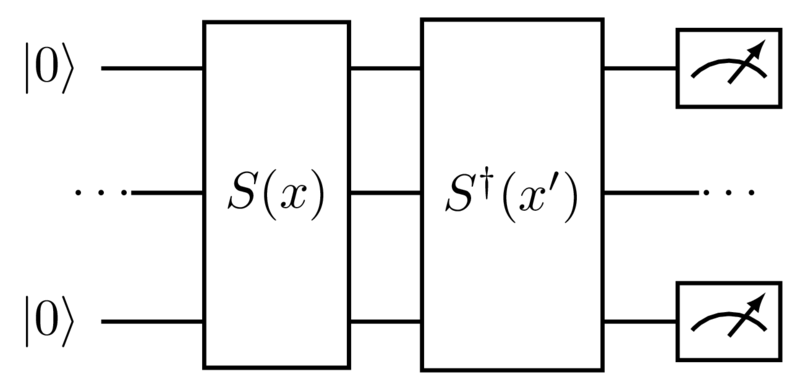
Интересно, что для этого метода есть теоретический результат, подкрепляющий его применение: оказывается, алгоритм Шора можно преобразовать в задачу машинного обучения, которую квантовый ядерный метод решает лучше классических.
Кодирование данных
Для кодирования данных применяются разные методы, среди них широко распространены:
- двоичное кодирование — binary encoding (число \(x\) кодируется своими битами \(x_i\)): \[ \ket{\psi(x)} = \otimes_{i=0}^m \ket{x_i}; \]
- амплитудное кодирование — amplitude encoding (вектор \(\vec{x} = (x_1, \dots, x_N) \in \mathbb{R}^N\) кодируется в амплитудах): \[ \ket{\psi(\vec{x})} = \frac{1}{\| x \|} \sum_{i=1}^N x_i \ket{i}; \]
- кодирование в углах — angle encoding (компоненты вектора \(\vec{x} = (x_1, \dots, x_N) \in \mathbb{R}^N\) кодируется поворотами соответствующих кубитов): \[ \ket{\psi(\vec{x})} = \prod_{i=1}^N \sigma_x^i(x_i) \ket{0}^{\otimes N}, \] где \(\sigma_x^i(\alpha)\) — поворот \(i\)-го кубита вокруг оси X (но можно использовать и другие оси) на угол \(\alpha\).