Однокубитные операции
Состояния и эволюция
Как уже говорилось на вводном занятии, квантовые системы можно описывать следующим образом: \[ \ket{\Psi} = \alpha \ket{0} + \beta \ket{1}, \] где \(\alpha, \beta \in {\mathbb C}\), \(\alpha^2 + \beta^2 = 1\). В этой системе два уровня (базовых состояния)
Аналогично описываются и многоуровневые системы: \[ \ket{\Psi} = c_0 \ket{0} + c_1 \ket{1} + \ldots + c_{N-1} \ket{N-1}, \] где \(c_j \in {\mathbb C}\), \(\sum_{j=0}^{N-1} c_j^2 = 1\)
Примеры
Частым примером квантовой системы является поляризация света. Направления стрелок обозначают направление поляризации: \[ \ket{\updownarrow} = \ket{0} \] \[ \ket{\leftrightarrow} = \ket{1} \]
При этом можно повернуть поляризацию и наблюдать: \[ \ket{\nearrow} = \frac{1}{\sqrt 2} \big( \ket{\updownarrow} + \ket{\leftrightarrow} \big) \] \[ \ket{\nwarrow} = \frac{1}{\sqrt 2} \big( \ket{\updownarrow} - \ket{\leftrightarrow} \big) \]
Если же внести мнимые компоненты, то получится круговая поляризация: \[ \ket{\circlearrowleft} = \frac{1}{\sqrt 2} \big( \ket{\updownarrow} + i \ket{\leftrightarrow} \big) \] \[ \ket{\circlearrowright} = \frac{1}{\sqrt 2} \big( \ket{\updownarrow} - i \ket{\leftrightarrow} \big) \]
Обозначения Дирака
Названия происходят от «bra-ket», т.е. «bracket»
Кет-вектор \[ \ket{\psi} = \alpha\ket{0} + \beta\ket{1} = \begin{pmatrix} \alpha \\ \beta \end{pmatrix} \]
Бра-вектор \[ \langle \psi | = \begin{pmatrix} \alpha^* & \beta^* \end{pmatrix} \]
Их скалярное произведение обозначается следующим образом. Скалярное произведение состояния на само себя равно единице: \[ \langle \psi | \psi \rangle = 1 \]
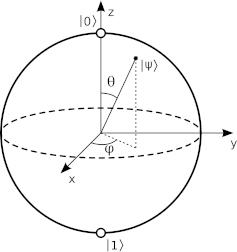
Сфера Блоха
Для наглядного представления о состояниях будет полезно использовать следующую визуализацию.
Как мы знаем, состояние кубита может быть представлено в виде
\begin{equation} |\Psi\rangle = \alpha_0 |0\rangle + \alpha_1 |1\rangle, \end{equation}где \(\alpha_k\) — комплексные числа.
Для комплексных чисел можно использовать полярное представление: \[ \alpha_k = r_k e^{i\phi_k}. \]
Вынося общий множитель \(e^{i\phi_0}\) за скобки и обозначая \(\Delta\phi = \phi_1 - \phi_0\), получаем:
\begin{equation} |\Psi\rangle = e^{i\phi_0} (r_0 |0\rangle + r_1 e^{i\Delta\phi} |1\rangle). \end{equation}Физические законы устроены таким образом, что глобальную фазу (множитель \(e^{i\phi_0}\)) невозможно измерить, возможно измерение только разницы фаз между состояниями 0 и 1, поэтому этот множитель можно игнорировать.
Кроме того, так как \(r_0^2 + r_1^2 = 1\), эти числа можно представить как, соответственно, косинус и синус какого-то угла: \[ r_0 = \cos \frac\theta 2; r_1 = \sin \frac\theta 2. \]
В итоге получаем следующее представление, которое зависит только от двух углов: \(\theta\) и \(\Delta\phi\):
\begin{equation} |\Psi\rangle = \cos \frac\theta 2 |0\rangle + e^{i\Delta\phi} \sin \frac\theta 2 |1\rangle. \end{equation}
Эти два угла задают точку на сфере. Эта сфера называется сферой Блоха:
Матрицы Паули
NOT
Одной из классических операций является операция «NOT». Она преобразует 0 в 1, и 1 в 0. Рассмотрим, как выглядит квантовый аналог этой операции.
Квантовый аналог NOT должен преобразовать состояние 0 в состояние 1, и наоборот. Для остальных векторов действие NOT будет получаться из линейности оператора.
Получаем, что для оператора NOT такая матрица: \[ NOT = \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} \]
Если посмотреть, как NOT действует на сфере Блоха, получим, что NOT задаёт поворот на 180 градусов вокруг оси X. Именно поэтому часто оператор NOT в квантовых схемах обозначают просто как \(X\).
Ещё одно обозначение этого оператора в схеме — крестик в кружке (как XOR):

Другие повороты на 180
Что получится, если рассмотреть повороты вокруг других осей? Оказывается, такие повороты задают другие операторы, которые тоже могут быть полезны.
Поворот вокруг оси Y задаётся следующей матрицей (проверьте!): \[ Y = \begin{pmatrix} 0 & -i \\ i & 0 \\ \end{pmatrix} \]
Аналогично, поворот вокруг Z задаётся следующей матрицей: \[ Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix} \]
Матрицы Паули
Эти матрицы поворотов вместе с единичной матрицей \(I\) называются матрицами Паули.
Этот набор матриц важен тем, что он является базисом для эрмитовых матриц \(2 \times 2\), т.е. при помощи этих матриц можно описать все возможные физические величины, которые можно наблюдать.
Напомним, что эрмитова матрица — самосопряжённая матрица: \(A^T = \bar{A}\), или \(A^\dagger = (\bar{A})^T = A\).
Операторы поворота
Что, если рассмотреть повороты на другие углы? Это можно сделать не только из общего интереса, но и из технологических соображений.
Часто для реализации какого-либо оператора, того же \(X\), физики используют какое-то континуальное управление, например, импульсы определённой длительности или магнитное поле необходимой силы. Если эти импульсы будут другой длительности, то вместо поворота на 180 градусов будет реализован поворот на какой-то другой угол, часто — зависящий от длительности. Таким образом, вместо одного оператора становится возможным реализовать сразу бесконечно много (с определённой точностью, конечно же).
Возвращаясь к математическим концепциям, повороты на произвольный угол \(\theta\) вокруг соответствующих осей можно задать как \[ R_x(\theta) = e^{-i\theta X/2}; \] \[ R_y(\theta) = e^{-i\theta Y/2}; \] \[ R_z(\theta) = e^{-i\theta Z/2}. \]
Разумеется, здесь возведение в экспоненту не поэлементное, а как матричная функция, т.е.: \[ e^A = I + A + \frac{A^2}{2!} + \frac{A^3}{3!} + \ldots \]
Таким образом, получаем следующие матрицы для поворотов (проверьте, что эти матрицы унитарны!): \[ R_x(\theta) = \begin{pmatrix} \cos \frac\theta 2 & -i \sin \frac\theta 2\\ i \sin \frac\theta 2 & \cos \frac\theta 2\\ \end{pmatrix} \] \[ R_y(\theta) = \begin{pmatrix} \cos \frac\theta 2 & -\sin \frac\theta 2\\ \sin \frac\theta 2 & \cos \frac\theta 2\\ \end{pmatrix} \] \[ R_z(\theta) = \begin{pmatrix} e^{-i \theta / 2} & 0 \\ 0 & e^{i \theta / 2} \\ \end{pmatrix} \]
Оператор Адамара
Ещё один важный оператор — оператор Адамара. Он «смешивает» состояние 0 и состояние 1. В итоге, далее мы получаем возможность одновременно вычислять преобразования для 0 и для 1 — т.н. «квантовый параллелизм».
Матрица оператора Адамара (Hadamard) \(H\) выглядит так: \[ H = \frac{1}{\sqrt 2}\begin{pmatrix} 1 & 1 \\ 1 & -1 \\ \end{pmatrix} \]
Посмотрим, что получается при двукратном применении оператора Адамара к состоянию 0:
\begin{equation*} |0\rangle \stackrel{H}{\mapsto} \frac{1}{\sqrt 2} (|0\rangle + |1\rangle) \stackrel{H}{\mapsto} \end{equation*} \begin{equation*} \stackrel{H}{\mapsto} \frac{1}{\sqrt 2} \Big( \frac{1}{\sqrt 2} (|0\rangle + |1\rangle) + \frac{1}{\sqrt 2} (|0\rangle - |1\rangle) \Big) = \end{equation*} \begin{equation*} = \frac{1}{2} \Big( |0\rangle + |1\rangle + |0\rangle - |1\rangle \Big) = |0\rangle. \end{equation*}Таким образом, после двукратного применения оператора Адамара получаем исходное состояние.
Рассмотрев таким же образом состояние 1, можно получить, что \(H^2 = I\).
Оператор изменения фазы
Ещё один важный с теоретической точки зрения вид операторов — оператор изменения фазы.
Если вы помните, любое однокубитное состояние мы представляли в следующем виде:
\begin{equation*} |\Psi\rangle = \cos \frac\theta 2 |0\rangle + e^{i\phi} \sin \frac\theta 2 |1\rangle. \end{equation*}Было бы полезно иметь возможность изменить угол \(\phi\) — фазу состояния. Для этого и предназначен оператор. В теории достаточно операторов \(S\) и \(T\), которые меняют фазу на \(\pi/4\) и \(\pi/8\): \[ S = \begin{pmatrix} 1 & 0 \\ 0 & i \\ \end{pmatrix} \] \[ T = \begin{pmatrix} 1 & 0 \\ 0 & e^{i \pi / 4} \\ \end{pmatrix} \]
Измерения
Измерения не являются унитарными преобразованиями и нарушают состояние квантовой системы.
Простейшим примером является измерение в базисе:
- состояние \[ \ket{\psi} = c_0 \ket{v_0} + c_1 \ket{v_1} + \ldots + c_{N-1} \ket{v_{N-1}}, \]
- результат измерения \({\mathcal M}\): \[ \Pr \Big[ {\mathcal M}\ket{\psi} = j \Big] = \big| \langle v_j | \psi \rangle \big|^2. \]
- после измерения переходит в состояние \(\ket{v_j}\)
Рассмотрим сумму вероятностей всех исходов: \[ \sum_{j=0}^{N-1} \big| \langle v_j | \psi \rangle \big|^2 = \sum_{j=0}^{N-1} \langle \psi | v_j \rangle \langle v_j | \psi \rangle = \langle \psi | \bigg( \sum_{j=0}^{N-1} | v_j \rangle \langle v_j | \bigg) | \psi \rangle = 1 \] Операторы \(| v \rangle \langle v |\) будут называться проекторами.
Более сложной версией можно считать измерение в произвольном базисе. Пусть даны произвольные операторы \({\mathcal M} = \{ \Pi_j \}\) с условиями:
- \(\Pi_j \Pi_k = 0\), если \(j \neq k\)
- ∑j Πj = I
Тогда результат измерения: \[ \Pr \Big[ {\mathcal M} \ket{\psi} = j \Big] = \langle \psi | \Pi_j | \psi \rangle. \] и после измерения состояние переходит в состояние: \[ \ket{\psi'} = \frac{\Pi_j \ket{\psi}}{\langle \psi | \Pi_j | \psi \rangle^{1/2}} \]
Другой способ описания измерений — наблюдамые. Пусть задана эрмитова матрица \(M\) — самосопряжённая матрица: \(M^T = \bar{M}\). Её можно привести к диагональному виду: \(M = U^\dagger D U\), \(D = \mathrm{diag}(\lambda_1, \ldots, \lambda_d)\).
Тогда с результатом измерения \(j\) будет связано собственное подпространство со значением \(\lambda_j\).
Пусть \(\ket{\psi}\) — состояние, а \(H\) — наблюдаемая. Тогда её матожидание: \[ E = \langle \psi | H | \psi \rangle \]
\[ \sum_j \langle \psi | \Pi_j | \psi \rangle \lambda_j = \langle \psi | \Big( \sum_j \lambda_j\Pi_j \Big) \ket{\psi} = \langle \psi | H | \psi \rangle. \]