Алгоритм Гровера
Задача поиска в неупорядоченной базе данных
В базе данных есть \(N\) записей, одну из которых требуется найти. Больше никакой информации (упорядоченность, наличие индексов и т.п.) о базе нет.
Классический алгоритм требует для решения этой задачи \(N\) запросов к базе.
Для квантового алгоритма информацию о БД требуется передать в схему. Как правило, для этого используют оракул, который получает на вход индекс \(i \in \{0,1,\ldots,N-1\}\) и изменяет фазу на противоположную, если соответствующая запись подходит. Пусть \(\omega \in \{0,1,\ldots,N-1\}\) означает индекс нужной нам записи:
\begin{equation*} U_\omega|x\rangle = -|x\rangle, \quad x=\omega \end{equation*} \begin{equation*} U_\omega|x\rangle = |x\rangle, \quad x\neq \omega \end{equation*}Идея решения
Алгоритм Гровера решает эту задачу итеративно: одна и та же операция выполняется несколько раз, каждый раз приближая состояние всей системы к состоянию-решению.
В качестве начального состояния выбирается наиболее запутанное состояние, создаваемое гейтами Адамара:
\begin{equation*} |\Psi_0\rangle = \frac{1}{N} \sum_{i=0}^{N-1} |i\rangle \end{equation*}Далее, на каждом шаге выполняются две операции: \(U_\omega\) и оператор Гровера.
Оператор Гровера состоит из:
- гейтов Адамара \(H^{\otimes n}\),
условного сдвига фазы — все базисные состояния, за исключением состояния 0, получают фазовый сдвиг \(-1\):
\begin{equation*} |0\rangle \mapsto -|0\rangle \end{equation*} \begin{equation*} |x\rangle \mapsto |x\rangle, \quad x\neq 0 \end{equation*}- гейтов Адамара \(H^{\otimes n}\).
Отражение относительно среднего
Выполнение шага итерации приводит к тому, что амплитуда отмеченного состояния увеличивается. Это можно наглядно увидеть, если рассматривать оператор Гровера как отражение относительно среднего.
Для примера, возьмём состояние, в котором у всех четырёх базисных состояний одинаковая амплитуда: \((1/2, 1/2, 1/2, 1/2)\), и отметим базисное состояние 1, т.е. поменяем его фазу: \((1/2, 1/2, -1/2, 1/2)\).
Если подсчитать, чему равно среднее значение всех амплитуд, получим \(1/4\). Оператор Гровера отражает все амплитуды относительно этого среднего: \((0,0,1,0)\). Разумеется, вероятность 1 получается не всегда, а только в некоторых случаях, но вероятность «попасть» в искомое состояние растёт:
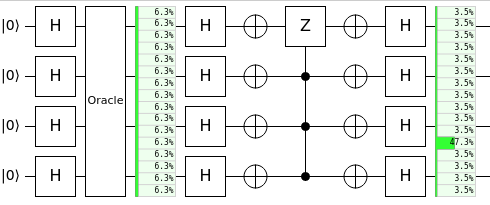
Количество итераций
Повторив этот шаг нужное количество раз, получим высокую вероятность измерить состояние, которое будет помечено.
Точно вычислить необходимое количество шагов можно геометрически. Для этого всё возможное пространство состояний представляется как плоскость, одна ось которого — искомое состояние \(\omega\), а другая — все остальные состояния \(\beta\).
Формально для произвольного состояния \(\psi\) выглядит так:
\begin{equation*} |\psi\rangle = \sum_{x=0}^{N-1} \alpha_x |i\rangle = \alpha_\omega |\omega\rangle + \sum_{x\neq\omega} \alpha_x |x\rangle = \alpha_\omega |\omega\rangle + b |\beta\rangle, \end{equation*}где состояние \(\beta\) определено как (нормирующий коэффициент — чтобы получить единичную длину)
\begin{equation*} |\beta\rangle = \frac{1}{\sqrt{N-1}} \sum_{x\neq\omega} |x\rangle. \end{equation*}Состояния \(\omega\) и \(\beta\) ортогональны друг другу.
При выполнении операций на каждом шаге текущее состояние \(\psi\) поворачивается в сторону состояния \(\omega\) на некоторый угол \(\theta\):
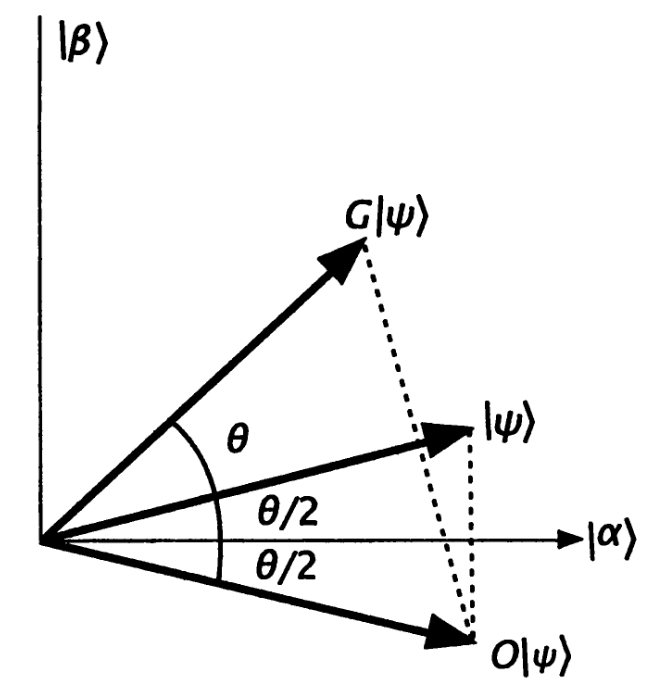
Можно вычислить угол \(\theta\), он оказывается равен \[ \theta = 2\arcsin \frac{1}{\sqrt{N}} \]
Поэтому после \(\frac{\pi\sqrt{N}}{4}) = O(\sqrt{N})\) итераций состояние окажется наиболее близко к искомому состоянию \(\omega\).
Оказывается, что эта оценка совпадает с нижней границей. Любой квантовый алгоритм, который получает информацию о базе данных только при помощи оракула \(U_\omega\), требует \(\Omega(\sqrt{N})\) запросов к нему, чтобы с большой вероятностью выдать правильный ответ.
Модификации
Несколько решений
Если у задачи не одно, а несколько решений (и нам известно их число \(M\)), то количество итераций несколько меняется, их должно быть \[ \frac{\pi}{4} \sqrt{\frac{N}{M}} \]
Неизвестное количество решений
Также алгоритм можно применять и для случая, когда количество решений неизвестно. Можно либо вначале оценить количество решений при помощи квантового алгоритма подсчёта и затем выполнить поиск Гровера для этого количества (такой алгоритм работает за \(O(\sqrt{N})\)), либо выполнить поиск несколько раз, считая, что количество решений \(M = N, N/2, N/4, \ldots, N/2^t, \ldots\).
Удовлетворение ограничений
Можно рассматривать алгоритм Гровера не как поиск в базе данных, а как поиск решения какого-либо уравнения \(f(x) = 1\), или задачу удовлетворения ограничений, которые задаются этим уравнением.
При этом вся база не копируется в квантовую память — это было бы слишком сложно и потребовало бы много усилий ради одного запуска, а наоборот, ограничения кодируются в оракуле.
Значение
Хотя алгоритмы Саймона, Шора и некоторые другие дают экспоненциальное ускорение по сравнению с классическими, при их решении квантовый алгоритм использует некоторую структуру, которая есть в пространстве решений.
Если о такой структуре неизвестно ничего, то лучшее, на что можно надеяться — это применение алгоритма Гровера, который даёт квадратичное ускорение. В частности, NP-полные задачи считаются сложными как раз потому, что для них неизвестна какая-либо структура, и наилучшим способом решения остаётся перебор всех вариантов. Поэтому, возможно, появление квантовых компьютеров и не поможет в решении NP-полных задач (если только не P=NP).
В то же время, для некоторых задач, например, задачи разложения на простые сомножители такая структура весьма неочевидна (впрочем, про задачу разложения на множители и не было доказано, что она NP-полна — т.е. что она эквивалентна любой другой NP-полной задаче по сложности). Обнаружение этой структуры хоть и не помогло найти алгоритм для классического компьютера, но позволило создать квантовый алгоритм решения этой задачи — алгоритм Шора.