Алгоритм Шора
Многие криптографические протоколы опираются на то, что число сложно разложить на простые множители (или сходные задачи). Алгоритм Шора позволяет сделать это за полиномиальное время, что экспоненциально быстрее классических алгоритмов (в худшем случае).
В классическом случае разложение числа \(n\) длиной \(m\) битов требует около \(n^{1/3} = 2^{m/3}\) шагов. Алгоритм Шора позволяет добиться того же результата за \(O(m^3)\) шагов.
Нахождение порядка
Пусть мы хотим найти простые сомножители положительного целого числа \(n\). Для простоты будем считать, что \(n = pq\), произведение двух простых чисел (как в RSA). Эту задачу можно свести к вычислению порядка мультипликативной группы \(\mathbb{Z}_n\).
Обозначим мультипликативную группу целых чисел по модулю \(n\) как \[ \mathbb{Z}^\times_n = \{x \in \mathbb{Z}_+: x < n, \gcd(x,n) = 1\}. \] Для заданного \(x \in \mathbb{Z}^\times_n\) нужно найти наименьшее такое \(r\), что \(x^r = 1 \pmod n\).
Если возведение в степень по модулю можно задать в виде квантовой схемы, то искомое \(r\) найдётся при помощи алгоритма оценки фазы — как период функции возведения в степень по модулю \(n\).
Имея же \(r\), нетрудно вычислить и множители \(n\).
Период и порядок
Из принципа Дирихле следует, что для любой группы \(G\) и элемента \(g \in G\) выполняется \(g^{|G|} = 1_G\). Но порядок \(r\) может быть меньше.
Например, для \(n = 15\) мультипликативная группа \(\mathbb{Z}^\times_{15} = \{1,2,4,7,8,11,13,14\}\) (можете проверить!), т.е. её размер \(|\mathbb{Z}^\times_{15}| = 8\). И, к примеру, для \(a = 7\) выполняется \(7^8 = 1 \pmod{15}\). Но, на самом деле, порядок числа 7 меньше, потому что \(7^4 = 1 \pmod{15}\).
При этом, если период \(a\) равен \(r\), то функция \(f_a(x) = a^x \pmod{n}\) является периодической с периодом \(r\): \[ 7^1 = 7; 7^2 = 4; 7^3 = 13; 7^4 = 1; 7^5 = 7; \ldots \pmod{n}. \]
Квантовый поиск периода
Для нахождения периода потребуется \(3q\) кубитов, где \(q\) такое, что \(n \le Q = 2^q < 2n\).
Выбираем случайным образом \(1 < a < n\) так, что \(\gcd(a,n) = 1\) (если это не так, то мы нашли делитель).
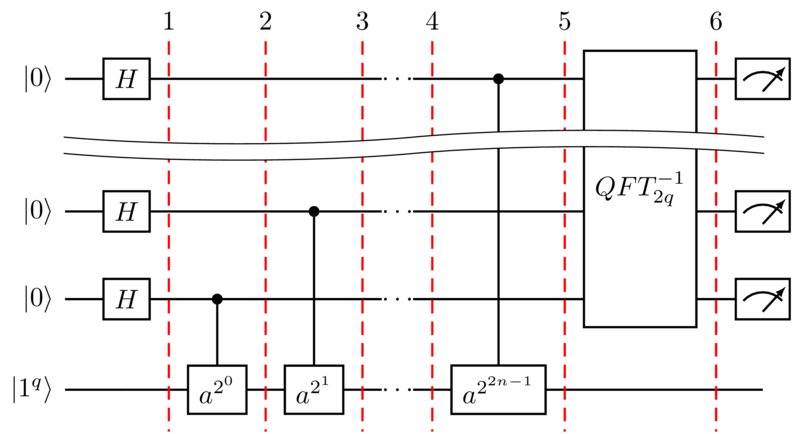
- Инициализируем кубиты в состоянии \[ \vert \Psi_1 \rangle = \frac{1}{\sqrt{Q}} \sum_{x=0}^{Q-1} |x\rangle \]
- Применяем возведение в степень \(x\) (последовательным возведением в квадрат): \[ \vert \Psi_5 \rangle = \frac{1}{\sqrt{Q}} \sum_{x=0}^{Q-1} |x\rangle |a^x \bmod n\rangle \]
- После обратного преобразования Фурье, получаем: \[ \vert \Psi_6 \rangle = \frac{1}{Q} \sum_{z=0}^{N-1} \sum_{y=0}^{Q-1} \Big[ \sum_{x\in\{0,\ldots,Q-1\}; a^x = z \bmod n} \omega^{xy} \Big] |y\rangle |z\rangle, \] где \(\omega = \exp(2\pi i/Q) \) — корень степени \(Q\) из единицы.
Можно показать, что при измерении будет выше вероятность тех состояний \(|y\rangle\), для которых \(yr/Q\) близко к целому числу.
Классическая пост-обработка
Остаётся по полученному \(y\) найти \(r\), и по нему — разложение \(n\) на множители.
Поскольку \(yr/Q\) близко к целому числу \(c\), то известное нам \(y/Q\) должно быть близко к \(c/r\). Можно найти такое приближение \(d/s\), что \(s < n\), и \[ \Big| \frac{y}{Q} - \frac{d}{s} \Big| < \frac{1}{2Q}. \]
Тогда найденное \(s\) будет близко к периоду \(r\), или будет его множителем. Перебрав несколько значений и проверяя, подходят ли они, получим \(r\) такой, что \(a^r = 1 \pmod{n}\) (если нет, то можем повторить квантовую часть ещё раз в надежде получить другое \(y\)).
Если мы получили нечётный \(r\), то мы тоже должны повторить квантовую часть с другим \(a\).
Пусть \(r\) — чётное. Обозначим \(b = a^{r/2} \bmod n\), причём \(b \neq 1\) (иначе период был бы \(r/2\)).
Получаем, что \(b^2 = 1 \pmod{n}\), или \[ b^2 - 1 = (b-1)(b+1) = cn \] для какого-то целого \(c\). Тогда получаем, что числа \(\gcd(n,b-1)\) и \(\gcd(n,b+1)\) являются делителями \(n\).