Многокубитные операции
Состояния сложных систем
Состояние сложной системы не всегда сводится к состоянию её подсистем: например, состояние \[\ket{\psi_{AB}} = \frac{1}{2}(\ket{10} + \ket{01})\] невозможно представить в виде \(\ket{\psi_{AB}} = \ket{\psi_A}\ket{\psi_B}\).
В общем случае, если состояния подсистем A и B описываются пространствами \({\mathcal H}_A\) и \({\mathcal H}_B\), то состояние системы будет описываться как \({\mathcal H}_A \otimes {\mathcal H}_B\), т.е. базисными векторами будут всевозможные комбинации базисных вектором подсистем A и B.
В результате каждый кубит, добавленный в систему, увеличивает вдвое количество её базисных состояний — количество состояний растёт экспоненциально.
Вычисления
Для использования квантовых компьютеров для вычислений следует понять, что ожидается в результате вычисления.
Как правило, для вычислений используются квантовые схемы, состоящие из проводов
и гейтов-операторов на них:
 Гейты выполняют операции на соответствующих кубитах.
Гейты выполняют операции на соответствующих кубитах.
Схемы можно комбинировать. Если две схемы нарисованы друг над другом, они запускаются одновременно на разных наборах кубитов (выполняется тензорное произведение соответствующих матриц преобразований). Если друг за другом — то вначале запускается схема слева, а затем схема справа (при этом начальным состоянием второй схемы становится состояние после завершения работы первой; иными словами матрицей преобразования такой схемы является обычное произведение матриц подсхем).
SWAP
Простейшим многокубитным оператором можно считать оператор SWAP. Он меняет местами значения двух кубитов. Конечно, можно считать, что это просто специально искривленные провода, но наличие оператора SWAP позволяет записать алгоритмы для некоторых архитектур квантовых компьютеров (обычно на сверхпроводниках), где невозможно связать два произвольных кубита, а многокубитовые операции должны производиться только над соседними кубитами.
Обозначения SWAP (если мы хотим подчеркнуть, что это гейт, или если хотим показать изменение порядка проводов):
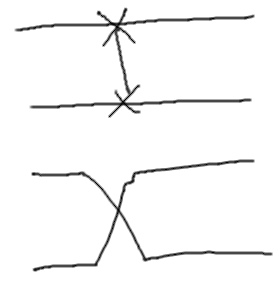
Матрицей SWAP-гейта будет такая: \[ SWAP = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \]
CNOT
Более интересным оператором является CNOT. Можно сказать, что это простейший вид условного оператора: если управляющий кубит установлен в 1, то к управляемому кубиту применяется оператор NOT; если управляющий кубит установлен в 0, то управляемый кубит не меняется.
Обозначение CNOT следующее (управляющий кубит отмечен черным кружком, на управляемом нарисован по сути NOT; управление обозначено вертикальной линией):
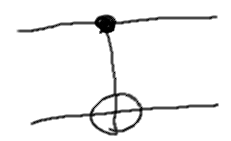
Матрица CNOT выглядит так: \[ CNOT = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} \]
Controlled-U
Аналогичным образом можно определить и более сложные условные операции, в которых к управляемым кубитам применяется не NOT, а произвольное унитарное преобразование \(U\).
Такие преобразования называют controlled-U, и на схемах обозначают следующим образом:
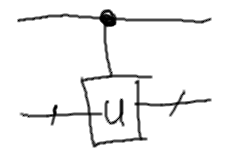
CCNOT
Что получится, если к двум управляемым кубитам применять CNOT? Получится CCNOT (или \(C^2NOT\)). Он преобразует базисные состояния так:
\begin{equation*} |110\rangle \mapsto |111\rangle; \end{equation*} \begin{equation*} |111\rangle \mapsto |110\rangle; \end{equation*}а для других комбинаций \(a,b,c \in \{0,1\}\)
\begin{equation*} |abc\rangle \mapsto |abc\rangle. \end{equation*}Обозначается CCNOT следующим образом:
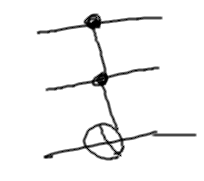
Аналогичным образом можно строить и операторы, где несколько кубитов управляют произвольным преобразованием \(U\).
Способы управления
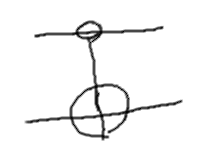
Похожим образом можно выполнять управление, когда преобразование выполняется, если управляющий кубит установлен в 0 (а не в 1, как было в прошлых гейтах).
На схеме в этом случае управляющий кубит обозначается пустым кружком. Вот, к примеру, так выглядит NOT, управляемый таким образом:
Теорема Соловэя-Китаева
Сколько всего возможно операторов, действующих на \(n\) кубитах?
Поскольку операторов столько же, сколько и унитарных матриц размера \(2^n \times 2^n\), и каждый элемент матрицы является комплексным числом, мы получаем, что их несчётное количество (что не означает, конечно, что их изучение займёт несчётное время).
Сколько всего возможно квантовых схем на \(n\) кубитах, содержащих известные нам одно- и многокубитные операторы?
Если исключить параметризованные операторы поворота на произвольный угол, таких схем будет счётное количество.
Как же получается, что нам достаточно только счётного количества схем из конечного числа операторов? Не должны ли мы изучать и изучать различные операторы на трёх, четырёх и большем количестве кубитов?
На этот вопрос отвечает теорема Соловэя–Китаева, которая гласит следующее.
Для произвольного наперёд заданного \(\epsilon > 0\) и для любого унитарного оператора \(U\) существует схема \(C\) глубины \(\log^{3.001} (1/\epsilon)\) такая, что \(\| C - U \| \le \epsilon\).
Эта схема \(C\) состоит только из гейтов CNOT, H, S и T.
Теорема приводится без доказательства, которое достаточно сложное. Желающих его изучить я отсылаю к книге Нильсена и Чанга.