Задания для решения в течение семестра

Написать функцию, которая создаёт схему для вычисления 3-КНФ (без отрицаний)

На входе задаётся список троек, которые задают дизъюнкции На выходе - схема cirq, которая вычисляет функцию

Например, [(1,2,3), (2,3,4)] задаёт функцию (x1 || x2 || x3) && (x2 || x3 || x4). Всегда ровно три литерала и все они положительные (нет отрицаний)

Реализуйте алгоритм Дойча-Йожи на cirq

Функция должна принимать оракул на вход (гарантируется, что он вычисляет либо константную, либо сбалансированную функцию)

Японский кроссворд - головоломка, в которой нужно закрасить некоторые клетки на прямоугольном поле. В качестве подсказок задаётся количество идущих подряд закрашенных клеток для каждой строки и для каждого столбца.

Написать на cirq оракула, которому задаётся набор подсказок для строк и столбцов японского кроссворда размером 3x3:

def nonogram_oracle(rows: List[List[int]], cols: List[List[int]]):
    pass

Например, параметра для следующего кроссворда будут равны (x - закрашенная клетка, . - пустая):

x.x | 1,1
.x. | 1
x.x | 1,1
----+
111
1 1

rows = [[1,1], [1], [1,1]]
cols = [[1,1], [1], [1,1]]

Элементы rows перечисляются сверху вниз, слева направо. Элементы cols перечисляются слева направо, сверху вниз

Реализовать на cirq алгоритм Гровера, который принимает на вход оракул и выдаёт решение (считайте, что у задачи ровно одно решение)

Проверьте, что этот код работает с оракулом из предыдущего задания.

Реализуйте алгоритм Саймона для нахождения периода функции, заданной оракулом.

Реализуйте квантовое преобразование Фурье

Найдите минимальное собственное число гамильтониана \[ H = 0.3980 Y \otimes Z - 0.3980 Z\otimes I -0.0113 Z\otimes Z + 0.1810 X\otimes X \]

В качестве анзатца можно выбрать схему из четырёх слоёв, в каждом из которых повторяется последовательно поворот вокруг оси Y, вокруг Z и CNOT:

Минимизацию можно выполнять произвольным образом, например, при помощи функции minimize библиотеки SciPy или любым другим образом.

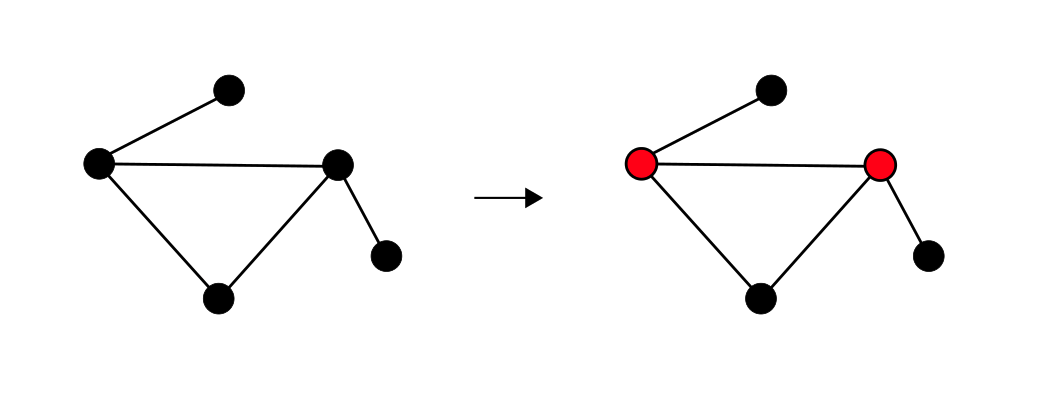
Создайте схему для QAOA и найдите минимальное вершинное покрытие графа на картинке. Ваш код должно быть просто адаптировать для любого другого графа

Реализуйте квантовый ядерный метод и классифицируйте ирисы Фишера при его помощи. Мы будем классифицировать первые два класса, т.е. 100 примеров.

Для подготовки данных используйте следующий код:

import numpy as np

from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler

X, y = load_iris(return_X_y=True)

# pick inputs and labels from the first two classes only,
# corresponding to the first 100 samples
X = X[:100]
y = y[:100]

# scaling the inputs is important since the embedding we use is periodic
scaler = StandardScaler().fit(X)
X_scaled = scaler.transform(X)

# scaling the labels to -1, 1 is important for the SVM and the
# definition of a hinge loss
y_scaled = 2 * (y - 0.5)

X_train, X_test, y_train, y_test = train_test_split(X_scaled, y_scaled)

Постройте схему для квантового ядра и используйте стандартные алгоритмы построения опорных векторов для их использования (предполагается, что kernel(x1,x2) — ваше ядро). Выведите точность вашего метода:

from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

def kernel_matrix(A, B):
    """Compute the matrix whose entries are the kernel
       evaluated on pairwise data from sets A and B."""
    return np.array([[kernel(a, b) for b in B] for a in A])

svm = SVC(kernel=kernel_matrix).fit(X_train, y_train)

predictions = svm.predict(X_test)
s = accuracy_score(predictions, y_test)
print(s)

Поскольку размерность мала, входные данные кодируйте в углах.